机器学习分类

监督学习（Supervised Learning）
无监督学习（Unsupervised Learning）
强化学习（Reinforcement Learning，增强学习）
半监督学习（Semi-supervised Learning）
深度学习（Deep Learning）

Python Scikit-learn

概述

一组简单有效的工具集
依赖Python的NumPy，Scipy和matplotlib库。
开源、可复用

常用函数

类别	应用（Applications）	算法（algorithm）
分类（classification）	异常检测，图像识别等	KNN，SVM等
聚类（clustering）	图像分割，群体划分等	K-Means，谱聚类等
回归（Regression）	价格预测，趋势预测等	线性回归，SVR等
降维（Dimension Reduction）	可视化	PCA，NMF等

理论知识深入资料

《机器学习》——周志华主页
《PRML》——Bishop 主页
《Machine Learning》——Andrew Ng
Coursera版
Stanford手书版
在线观看
 课程主页
《CS231n》——李飞飞
课程主页
 在线观看
《Reinforcement Learning》——David Silver
课程主页
 在线观看

Sklearn标准库的基本功能

分类模型

分类模型	加载模块
最近邻算法	neighbors.NearestNeighbors
支持向量机	svm.SVC
朴素贝叶斯	naive_bayes.GaussianNB
决策树	tree.DecisionTreeClassifier
集成方法	ensemble.BaggingClassifier
神经网络	neural_network.MLPClassifier

回归任务

回归模型	加载模块
岭回归	linear_model.Ridge
Lasso回归	linear_model.Lasso
弹性网络	linear_model.ElasticNet
最小角回归	linear_model.Lars
贝叶斯回归	linear_model.BayesianRidge
逻辑回归	liner_model.LogisticRegression
多项式回归	preprocessing.PolynomialFeatures

聚类任务

聚类方法	加载模块
K-means	cluster.KMeans
AP聚类	cluster.AffinityPropagation
均值漂移	cluster.MeanShift
层次聚类	cluster.AgglomerativeClustering
DBSCAN	cluster.DBSCAN
BIRCH	cluster.Birch
谱聚类	cluster.SpectralClustering

降维任务

降维方法	加载模块
主成分分析	decomposition.PCA
截断SVD和LSA	decomposition.TruncatedSVd
字典学习	decomposition.SparseCoder
因子分析	FactorAnalysis
独立成分分析	FastICA
非负矩阵分解	NMF
LDA	LatentDirichletAllocation

无监督学习

概念

利用无标签的数据学习数据的分布或数据与数据之间的关系被称作无监督学习。

特点

有监督学习和无监督学习的最大区别在于数据是否有标签。
无监督学习最常应用的场景是聚类（clustering）和降维（Dimension Reduction）

聚类

概念

聚类，就是根据数据的“相似性”将数据分为多类的过程。
评估两个不同样本之间的“相似性”，通常使用的方法是计算两个样本之间的“距离”。使用不同的方法计算样本见的距离会关系到聚类结果的好坏。

距离计算方法

sklearn.cluster

sklearn.cluster模块提供的各聚类算法函数可以使用不同的数据形式作为输入

标准数据输入格式：[样本个数，特征个数]定义的矩阵形式。
相似性矩阵输入格式：即由[样本数目]定义的矩阵形式，矩阵中的每一个元素为两个样本的相似度，如DBSCAN，AffinityPropagation(近邻传播算法)接受这种输入。如果以余弦相似度为例，则对角线元素为1,。矩阵中每个元素的取值范围为[0,1]。

算法名称	参数	可扩展性	相似性度量
K-means	聚类个数	大规模数据	点间距离
DBSCAN	领域大小	大规模数据	点间距离
Gaussian Mixtures（高斯混合模型）	聚类个数及其他超参	复杂度高，不适合处理大规模数据	马氏距离
Birch	分支因子，阈值等其他超参	大规模数据	两点间的欧式距离

降维

概念

降维，就是在保证数据所具有的代表性特性或者分布的情况下，将高维数据转化为低维数据的过程。
常应用于：

数据的可视化
精简数据

sklearn.decomposition

算法名称	参数	可扩展性	适用任务
PCA	所降纬度及其他超参	大规模数据	信号处理等
FastICA	所降纬度及其他超参	超大规模数据	图形图像特征提取
NMF	所降纬度及其他超参	大规模数据	图形图像特征提取
LDA	所降纬度及其他超参	大规模数据	文本数据，主题挖掘

聚类之K-Means+31省市居民家庭消费调查

K-Means聚类算法

K-Means算法以K为参数，把n个对象分成k个簇，使簇内具有较高的相似度，而簇间的相似度较低。
步骤：

随机选择k个点作为初始的聚类中心
对于剩下的点，根据其与聚类中心的距离，将其归入最近的簇。
对每个簇，计算所有点的均值作为新的聚类中心。
重复2、3直到聚类中心不再发生变化。

代码

//1、建立工程，导入sklearn相关包
import numpy as np
from sklearn.cluster import KMeans
//2、加载数据，创建K-means算法实例，并进行训练，获得标签
if __name__=='__main__':
    data,cityName = loadData('city.txt')//读取数据
    km = KMeans(n_cluster=3)//计算
    label = km.fit_predict(data)//计算
    expenses=np.sum(km.cluster_centers_,axis=1)//数字加和
    #print(expenses)
    CityCluster=[[],[],[]]
    for i in range(len(cityName)):
        CityCluster=[label[i]].append(cityName[i])
    for i in range(len(CityCluster)):
        print("Expenses:%.2f"% expenses[i])
        print(CityCluster[i])

调用K-Means方法所需要的参数：

n_clusters：用于指定聚类中心的个数
init：初始聚类中心的初始化方法
max_iter：最大的迭代次数
一般调用时只用给出n_clusters即可，init默认是K-Means++，max_iter默认是300

其他参数：

data：加载的数据
label：聚类后各数据所属的标签
fit_predict()：计算簇中心以及为簇分配序号

loadData函数：

def loadData(filePath):
    fr=open(filePath,'r+')
    lines=fr.readlines()
    retData =[]
    retCityName =[]
    for line in lines:
        items = line.strip().split(",");
        retCityName.append(items[0])
        retData.append(float(items[i]))
    for i in range(1,len(items))
        return retData,retCityName

拓展和改进

计算两条数据相似性时，Sklearn和K-Means默认用的是欧式距离。虽然还有余弦相似度，马氏距离等多种方法，但没有设定计算距离方法的参数。因此只能通过修改K-Means的源代码。

DBSCAN方法及应用

概念

DBSCAN密度聚类
DBSCAN算法是一种基于密度的聚类算法：

聚类的时候不需要预先指定簇的个数
最终的簇的个数不定

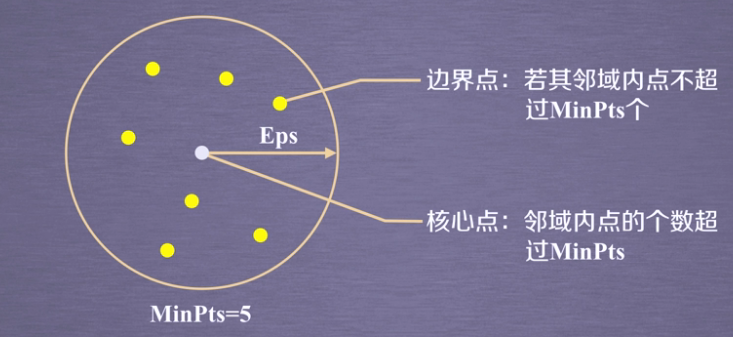
将数据点分为三类，分别是：

核心点：在半径EPS内含有超过MinPts数目的点。
边界点：在半径Eps内点的数量小于MinPts,但是落在核心点的领域内。
噪音点：既不是核心点也不是边界点的点。

DBSCAN算法流程

将所有点标记为核心点、边界点或噪声点
删除噪声点
为距离在Eps之内的所有核心点之间赋予一条边
每组连通的核心点形成一个簇
将每个边界点指派到一个与之关联的核心点的簇中（哪一个核心点的半径范围之内）

DBSCAN的应用实例

实验目的

通过DBSCAN聚类，分析学生上网时间和上网时长的模式。

技术路线

sklearn.cluster.DBSCAN

步骤

建立工程，导入sklearn相关包

1 2	import numpy as np from sklearn.cluster import DBSCAN

DBSCAN主要参数：

eps：两个样本被看作邻居节点的最大距离
min_samples：簇的样本数
metric：距离的计算方法

1	sklearn.cluster.DBSCAN(eps=0.5,min_sample=5,metric='euclidean') #欧氏距离

读入数据并进行处理

import numpy as np
import sklearn.cluster as skc
from sklearn import metrics
import matplotlib.pyplot as plt

mac2id=dict()
onlinetimes=[]
f=open('TestData.txt')
for line in f:
    mac=line.split(',')[2] #读取数据Mac地址
    onlinetime=int(line.split(',')[6]) #开始上网时间
    starttime=int(line.split(',')[4].split(' ')[1].split(':')[0]) #上网时长
    if mac not in mac2id:
        mac2id[mac]=len(onlinetimes) 
        onlinetimes.append((starttime,onlinetime))
    else:
        onlinetimes[mac2id[mac]]=[(starttime,onlinetime)]
    real_X=np.array(onlinetime).reshape((-1,2))

上网时间聚类，创建DBSCAN算法实例，并进行训练，获得标签

X=real_x[:,0:1]

# 调用DBSCAN方法进行训练，labels为每个数据的簇标签
db=skc.DBSCAN(eps=0.01,min_samples=20).fit(X)
labels=db.labels_

# 打印数据被记上的标签，计算标签为-1，即噪声数据的比例
print('Labels:')
print(labels)
ratio=len(labels[label[:]==-1])/len(labels)
print('Noise ratio:',format(ratio,'.2%))

# 计算簇的个数并打印，评价聚类效果
n_clusters_ =len(set(labels))-(1 if -1 in labels else 0)
print('Estimated number of clusters: %d' % n_clusters_)
print("Sihouette Coefficent: %0.3f'% metrics.silhouette_score(x,labels))# 计算轮廓系数（silhouette Coeffient）：类的密集与分散程度的评价指标

# 打印各簇标号以及各簇内的数据
for i in range(n_clusters_):
    print('Cluster', i, ':')
    print(list(X[labels==i].flatten())) 
#flatten()函数是为了返回一个折叠成一维的数组。如array([[1,2],[3,4],[5,6]]) >>>a.flatten()->array([1,2,3,4,5,6])

输出标签，查看结果

画直方图，分析实验结果

转换直方图分析

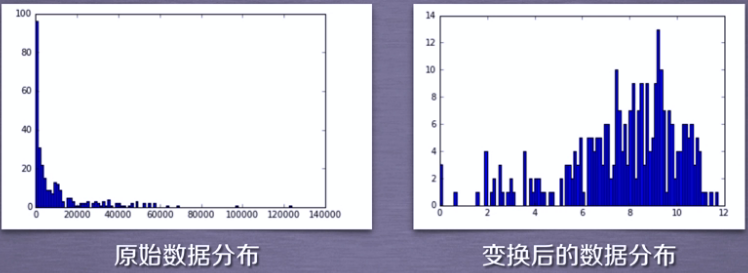
1 2	import matplotlib.pyplot as plt plt.hist(X,24)

观察：上网时间大多聚在22：00和23:00
注意：为了使数据展示更加直观，可以使用对数变换技巧使直方图更直观

无监督学习——降维

目的：学习PCA方法及其应用

主成分分析PCA

主成分分析（Principal Component Analysis，PCA）是最常用的一种降维方法，通常用于高维数据集的探索与可视化，还可以用作数据压缩和预处理。
PCA可以吧具有相关性的高维变量合成为线性无关的低维变量，称为主成分。主成分能够尽可能保留原始数据的信息。

机器学习北京理工大学公开课